
Developmental dyscalculia is a specific, severe, and persistent difficulty in understanding numbers. Affecting 3–10% of the population, it often co-occurs with other learning difficulties. Here are six tried-and-tested steps to help overcome dyscalculia.
Overview of dyscalculia
Dyscalculia often runs in families, suggesting a genetic component. It is also linked to deficits in cognitive skills and numerical processing, with strong evidence of malformations in the brain’s right parietal lobe.
The most widely agreed-upon characteristics of dyscalculia are (1) difficulty learning and remembering arithmetic facts and (2) difficulty carrying out calculation procedures, often with immature problem-solving strategies, slow solution times, and high error rates. Other symptoms include (3) poor number sense and (4) an inability to subitize (perceive small quantities without counting).
Numeracy is essential for survival in society. Whether in daily living, work, or leisure, we cannot escape the use of numbers. Every job requires math, from farming to rocket science. The effects of mathematical failure can seriously limit career and life choices. It may close the door on a student’s vocational dreams and undermine aspirations to become a teacher, engineer, or doctor. Math is needed no matter what language you speak or the country in which you live.
Dyscalculia cannot be corrected with medication. Instead, specialized differentiation strategies are required to support learners. Below are six tried-and-tested steps to overcoming difficulties in mathematics.
1. Teach step-by-step
Specific skills must be mastered before new ones can be learned. For example, a child is trained to pass, control, dribble, and shoot the ball before learning to play soccer. Without these foundational skills, they will have two left feet on the soccer field. The same applies to math.
Foundational brain-based skills required for mathematics include visuospatial skills, sequential memory, procedural memory (the memory of how to perform certain routines or tasks), working memory (the ability to hold and manipulate information mentally), and logical thinking.
In addition, foundational math skills include counting and skip-counting. The role of counting in math can be compared to the role of letter-sound relationships in reading. Other essential math skills are understanding place value and performing simple addition, subtraction, multiplication, and division.
2. Teach in a multi-sensory way
Information enters the brain through three main channels: visual, auditory, and kinesthetic. Children with learning challenges are often weaker in one or two of these areas. A multi-sensory teaching style allows stronger channels to support the weaker ones (Hornigold, 2015).
The cone of learning illustrates this well: we remember 10% of what we read, 20% of what we hear, 30% of what we see, 50% of what we see and hear, and 70–100% of what we hear, see, say, and do.
The Concrete, Pictorial, Abstract approach (CPA) is a multi-sensory method that works particularly well in helping dyscalculic students grasp complex math concepts. It consists of three stages:
- Concrete — the “doing” stage, where students use physical objects to solve problems, e.g., arranging four rows of seven blocks to represent 4 × 7.
- Pictorial — the “seeing” stage, bridging concrete and abstract understanding through pictures, diagrams, or models. For the 4 × 7 example, students draw four rows of seven blocks.
- Abstract — the “symbolic” stage, where students solve problems using symbols alone, e.g., working out 4 × 7 without visual aids.
3. Don’t be afraid of repetition
The word repetition comes from the Latin repetere, meaning “to do or say again.” Rote is the outcome of repetition — responding automatically by memory alone, without thought. Repetition and drill-and-practice lead to fast, effortless, and automatic processing.
Knowledge stored in long-term memory is often needed as a stepping-stone to deeper understanding. This makes drill-and-practice essential to academic performance, just as it is to the performance of a virtuoso violinist. A meta-analysis by Swanson and Sachse-Lee (2000) of 85 academic intervention studies found that the largest effect sizes were obtained by interventions that included systematic drill, repetition, practice, and review.
From a neuroscientific perspective, repetition is vital for “wiring” the brain — forming synapses or connections between brain cells. Without repetition, key synapses do not form.
4. Construct a “pyramid of repetition”
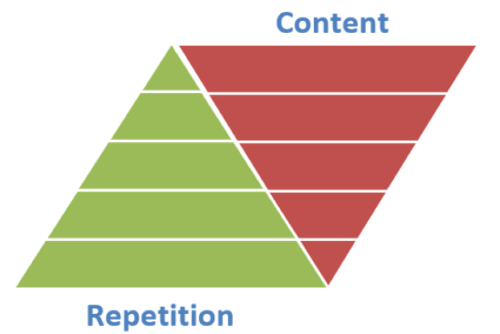
Mere repetition, however, is not enough. A “pyramid of repetition” must be built for the beginner learner.
This principle comes from the work of Shinichi Suzuki, a Japanese violinist, educator, and founder of the international Suzuki method of music education. In his book Nurtured by Love, Suzuki explains that the beginner must start by repeating a small amount of material over and over. Gradually, less repetition is needed to master new skills and knowledge.
In dyscalculia intervention, a “pyramid of repetition” can be applied to develop both foundational brain-based skills and math skills.
5. Minimize anxiety
Students with dyscalculia are prone to math anxiety, an adverse reaction to mathematics associated with negative emotions. When required to solve mathematical problems, people with dyscalculia may experience feelings of tension, helplessness, mental disorganization, and dread. In extreme cases, this can even cause a phobia of mathematics and mathematical devices.
It is crucial to minimize anxiety levels as much as possible. Anxiety causes heart rate and blood pressure to increase, switching the body to “fight or flight” mode. Math anxiety may fill up the brain’s working memory space, preventing the complete and effective processing of numerical tasks (Ashcraft et al., 2000).

Scaffolding is an effective teaching technique that enables students to build confidence in a new skill. A teacher or parent provides high-level support when introducing or applying a new skill, and then gradually withdraws support as the student becomes more confident. In a scaffold approach, a teacher typically links new knowledge to prior knowledge through questioning, pre-teaching of vocabulary, and by providing familiar examples before introducing unfamiliar elements.
Modeling is another effective way to teach new calculation methods. For example, when introducing long division, the teacher first demonstrates the calculation while talking through the steps. Then, several examples are worked through with the students, where they guide the teacher through the process. Next, individual students complete examples on the board with the teacher’s support. Finally, learners work through equations independently.
6. Embrace flearning
Flearning — learning from failure — is a new term that highlights how individuals can grow by learning from mistakes.

Everyone makes mistakes, and mistakes are vital for developing understanding. Research at Stanford University has shown that synapses in the brain grow when mistakes are made, even if those errors are not corrected. It is the struggle to reach the correct answers that fosters growth. However, there is no growth when the answers are already correct.
Unfortunately, constantly making mistakes in math can lead some children to give up. One of the most powerful moves a parent or teacher can make is to change the message around wrong answers. Teaching students that mistakes are positive can have an incredibly liberating effect. For this to work, however, students must feel safe to make mistakes.
One way to achieve this is to focus on identifying and correcting misconceptions rather than on the right answer. Another is to guide students toward self-correction through leading and probing questions, drawing their attention to the part that did not work. This helps them question their own thinking and search for new understanding.
Overcoming dyscalculia symptoms
The above steps are essential in helping students overcome dyscalculia. Watch three families’ struggles and their eventual triumph over dyscalculia. Then book a free consultation to discuss your child’s learning needs.
Overcoming Dyscalculia Symptoms: 6 Tried and Tested Steps was authored by Hannelie Brönner and Sue du Plessis. Hannelie is a secondary math and remedial teacher who worked in the UK for 17 years as a remedial teacher and SENDCo at mainstream schools before becoming the Head of School at Starhurst School, a special secondary school for boys with SEMH needs. She holds an MA Ed (Leadership and Management), specialising in Inclusive Education. Sue du Plessis (B.A. Hons Psychology; B.D.) is an educational specialist with 30+ years of experience in learning disabilities.
References for Overcoming Dyscalculia Symptoms: 6 Tried and Tested Steps:
- Ashcraft, M. H., Kirk, E. P., & Hopko, D. (2000). On the cognitive consequences of mathematics anxiety. In C. Donlan (Ed.), The Development of Mathematical Skills (pp. 197–222). Hove: Psychology Press.
- Hornigold, J. (2015). Dyscalculia Pocketbook. Alresford, Hampshire: Teachers’ Pocketbooks.
- Suzuki, S. (1993). Nurtured by Love (2nd ed.). USA: Summy-Birchard, Inc.
- Swanson, H. L., & Sachse-Lee, C. (2000). A meta-analysis of single-subject-design intervention research for students with learning disabilities. Journal of Learning Disabilities, 33(2), 114–136.


